수학으로 영어하자! : 1편 사각형 - 사다리꼴, 등변 사다리꼴, 평행사변형, 마름모, 직사각형, 정사각형의 의미를 영어 어원으로 잡아보자!
제가 예전에
수학으로 영어를 하면 어떨까요? 글을 올리면서
저만 좋아할 것 같다고 ㅋㅋ
근데 드디어 그 저만 좋아할 포스팅을 올리고 있습니다! ㅋㅋ
이런 이기적인!!!!!
근데 정말
수학으로 영어를 하면 특히 어원에서 도움을 참 많이 받을 수가 있어요.
영어의 주인은 그림인데
도형은 그림이 곧 이름인 친구잖아요?
그래서 이름만 잘 알아도
우리가 정말 쉽게 그림을 그릴 수 있습니다.
그러니 꼭 함께 해주셨으면 좋겠어요^^
그럼 달려보겠습니다!
Go go go!
01. 사각형의 종류

우선 사각형의 종류인데요.
Brit) Irregular Quadrilateral - Trapezium - Isoscles Trapezium -
Amer) Trapezium - Trapezoid - Isoscles Trapezium -
공통) Parallelogram - kite - Rhombus - Rectangle - Square
그림이 곧 이름이다! - 라고 말씀드렸죠?
그래서 저 친구들의 이름을 따로 적지는 않겠습니다. 보면 아실테니.
대신 왜 저 이름인가?
그림 -> 이름 / 이름 -> 그림이 어떻게 완벽하게 이루어지는가!
오늘은 이 점에 중점을 두어서 한번 가보도록 하겠습니다.
그냥 제가 좋아하는 어원 찾기예요^^

quadrilateral = quadri (four) + lateral (side)
=> four sides => 네 개의 선분으로 이루어진 도형 => 4변형.
선분 4개로 만들 수 있는 가장 기본적인 도형의 형태죠?
그리고 아주 크게 irregular / regular 로 나뉠 수 있는데
우리는 저 그림을 통해서 regular 의 이미지를
그려내는데 도움을 받을 수 있습니다!

regular quadrilateral 이라고 하면
바로 square 입니다.
왜?
선과 각이 모두 어떤 규칙을 따르고 있기 때문입니다.
1) 선의 규칙 : 네 변의 길이가 같음
2) 각의 규칙 : 네 각의 크기가 90도로 같음.
이런 규칙 내에 존재해야 regular 라는 말을 쓸 수 있는 겁니다.
regular polygon 도 마찬가지예요.
선과 각의 규칙을 지키고 있다는 거죠.
그리고 regular member? - 정규 멤버들이 지켜야 할 규칙이 따로 있겠죠?
이렇게 rule 내에 존재해야 비로소
regular 라는 이름을 붙일 수 있습니다.
그림에서 첫번째 친구는 선과 각의 규칙을 모두 어겼죠?
그래서 irregular 이고
저 그림들은 irregular -> regular 로 진화하고 있습니다!
그쵸?

이 친구 역시 irregular quadrilateral 이 맞아요
아직 정사각형이 아니니까요!
그리고 뒤에서 다시 보게 되겠지만
tra 라는 단어가 four 이라는 의미를 주고 있습니다.
연상할 수 있는 그림은 테이블?
그 정도겠네요.

having only sides parallel and two not
오직 한 쌍만 평행한 사변형입니다.
우리는 이 친구를 사다리꼴이라고 부르죠?
점점 regular 를 향해서 가고 있습니다!

having two equal sides
isos : equal, identical
자! 평행이라는 조건을 만족시켰으니
이제는 등변! 즉 길이가 같은 사변형이 등장하게 됩니다!
이름하여 등변 사다리꼴!
한 쌍이 평행하고, 평행하지 않은 두 변의 길이가 같죠?
이게 이름에 그대로 있는 거예요!
꼭 독어 보는 것 같죠? 의미를 다 나열해서 단어 만드는 것 같은..
예를 들어 볼펜!
Kugelschreiber : kugel (둥근, 공 : ball) + schreiben (쓰다 : scribe, write)
끝부분이 둥글게 생긴 필기구!
뭐 이렇게 기억하는데... (아마 맞을 거에요)
이렇게 이름이 다 하잖아요!
이름이 그림을 바로 만들어내잖아요?
이래서 어원 공부가 중요합니다!
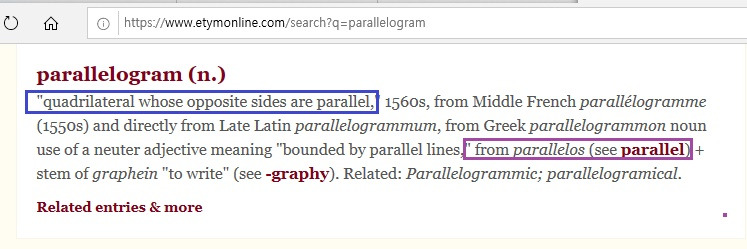
quadrilateral whose opposite sides are parallel
그리고 사다리꼴에서 좀더 진화해서
이번엔 마주 보는 두 쌍이 평행한 사변형이 나타났습니다!
이 친구가 평행사변형이예요.
그리고 평행이라는 성질때문에
등변 사다리꼴에서부터 엇각 / 동위각 을 이용해서 각의 크기가 같은 두 쌍이 각각 만들어지긴 하는데
이게 이름엔 아직은 등장을 안해요
아직은 선분입니다!
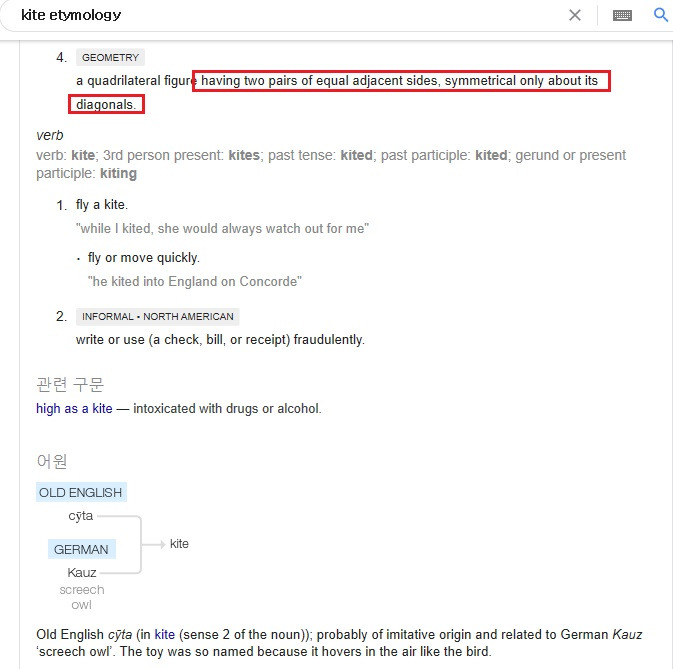
having two pairs of equal adjacent sides, symmetrical only about its diagonals.
아까는 opposite!
즉! 마주 보는 변들이 평행했는데요.
이번엔 이웃하는 변들의 길이가 같아요!
평행과는 상관이 없고 길이가 같다! - 이렇게 이동하게 됩니다.
이 역시 regular 가 갖춰야 하는 rule 중에 하나죠?
이렇게 하나씩 하나씩 갖춰가고 있습니다.
그리고 diagonal 이란 말이 나왔는데
dia + gonal 이예요.
이 친구도 한번 볼게요.
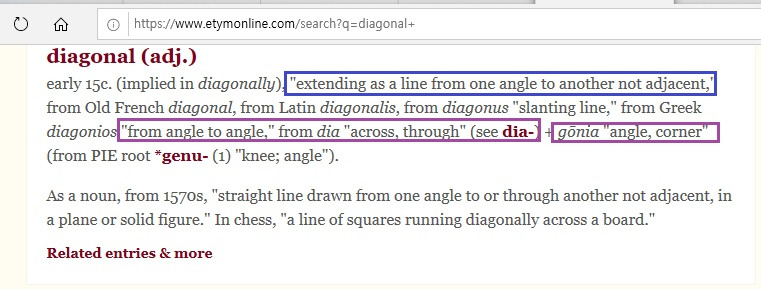
diagonal = dia (through) + agonal (angle)
= from angle to angle.
= extending as a line from one angle to another not adjacent.
한 각에서 이웃하지 않은 각까지 선을 그어본다 생각하면?
그게 바로 대각선이죠?
여기서 대각선의 개념이 나오기 시작합니다!
이 친구가 대각선 대칭이기 때문에
dia 라는 개념은 이미 익숙하실 거예요.
지름이 diameter 이잖아요? 그쵸?
이 친구가 diameter 이잖아요?
가로질러 중심을 지나는!
그리고 반지름은 radius
근데 오늘은 이 친구가 주인공이 아니니까 그냥 참고로만!
그래서 dia = through 로 잡아놓으시면 편해요!
뭐가? 그림 그리기가^^

드디어 이 친구!
마름모 친구까지 왔습니다!
a parallelogram with opposite equal acute angles, opposite equal obtuse angles, and four equal sides.
평행사변형에서 출발해서
마주 보는 각의 크기가 한 쌍은 예각 / 한 쌍은 둔각 이렇게 같고
가장 중요한 것!
네 변의 길이가 모두 같습니다!
그리고 acute <-> obtuse!
이 친구들의 어원이 acute (sharp) <-> obtuse (dull) 입니다!
그래서 예각 / 둔각 이라는 이름이 붙었어요.
번역 그대로죠? ㅋㅋ

그리고 rhombus 는 어원 자체가 마름모꼴이란 뜻인데
spinning top 과 turn, twist, bend 를 어떻게 연결시킬 수 있을까요?
마름모는 네 변의 길이가 모두 같잖아요 그쵸?
그럼 이 친구를 좌표평면 위에 올려보면 뭔가 나오지 않을까요?

맨 꼭대기의 좌표는 (0, y)
왼쪽의 좌표는 (-x, 0)
오른쪽의 좌표는 (x, 0)
맨 아래의 좌표는 (o, -y)
이렇게 서로 대칭을 이루고 있기 때문에
대칭을 이루고 있는 점끼리 바꿔도 그림은 바뀌지 않는다는!
뭐 이런 걸 마름모 생각할 때 고려한 게 아닌가
즉! 뒤집어도 같은 모양!
전 이렇게 마름모를 이해해봤습니다!
이러면 축 중심으로 돌 수 있고
뒤집어도 같은 그림! 접으면 일치하고!
그리고 축을 중심으로 실같은 것을 같으면
사용되는 실의 양이 일치하는! (평면이니까 실을 잘라 붙이는 걸로?)
근게 이 감다! 라는 말이 twist 거든요!
이렇게 spin / turn / twist / bend 를 묶어서 마름모를 이해해보려고 시도해봤습니다.
도움이 좀 되시나요?
전 솔직히 너무 잼나요!!!
진짜 좋아하는 수학이랑 영어라서 끊을 수가 없네 ㅋㅋ
오늘 사변형 -> 사각형은 끝내도록 하겠습니다
에헴~
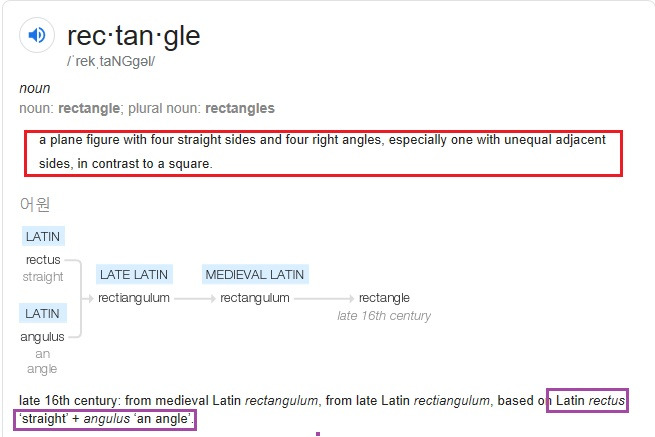
이제 각 (angle) 님이 나오셨습니다!
recangle = rect (rectus : stright) + angle (angulus : angle)
a plane figure with four straight sides and four right angles, especially one with unequal adjacent sides, in contrast to a square
네 각지 모두 직각이지만
네 변이 모두 같은 것은 아닌! 대변 (마주 보는 변) 의 길이만 각각 같은!
이 친구가 직사각형 입니다!
평행사변형까지는 확실히 변의 성질이었는데
마름모에서 좀 종합적으로 갔다가
직사각형부터는
'각'이 이름 속으로 들어갑니다!
변 -----> 각의 이동이죠!
직각이면 평행과 등변의 조건이 성립할 수 밖에 없어요!
얘만 애기해줘도 된다! 이 자신감!
너무 사랑스럽지 않아요?
막 귀여운 것 같애 ㅋㅋ
그리고 끝판왕 갑니다!

a plane figure wih four equal straight sides and four right angles.
드디어 네 변과 네 각을 모두 갖췄습니다!
이렇게 모든 조건을 갖췄기 때문에
처음에 말씀드린
regular quadrilateral 이 되는 것입니다!

그래서 이름 자체가 사각형의 완성형입니다!
사각형이 갖출 수 있는 모든 조건을 갖추게 되면
이렇게 정사각형이 될 수 있고
이렇게 사각형의 진화가 완성될 수 있습니다.
너무 수고 많으셨습니다!!!!!
사변형 (사각형) -> 정사각형 에 이르기까지
조건 하나하나 갖춰가는 우리 친구들을 보면서
어떤 생각이 드셨나요?
저는 이게 세상의 이치인 것 같습니다.
하루 아침에 세상이 정의로워질 수는 없는 것 같아요.
사변형 (사각형) 친구들도 하나한 조건을 갖춰나가면서 이렇게 진화했듯이
사회 역시 이런 ㅘ정을 거쳐가면서 정의로 한 발자국씩 나아갈 수 있는 게 아닐까요?
그래서 지금 100% 정의롭지 않다고 해서 실망하지 않으려고 합니다.
대신 기대를 걸어보겠습니다! 점점 수학처럼 진화해나갈 이 사회에!
그리고 저도 계속 열심히 진화해나가보도록 하겠습니다!
진정한 regular 가 되는 날까지!
done for today!
brought to you by Lesmy!
take care!
레미였습니다!
감사합니다!
행복합시다!!!!!
정의를 기다리며!!!

다각형도 나중에 해볼까?
잼날 듯...



