오늘 포스팅 주제는
초등 5학년 수학 기초
평행사변형 넓이 공식
중등 수학 중학 수학
중3 수학 삼각비 특수각
인데요
제가 원래
고등학교 2학년 1학기 때까지
가+장 좋아하는 과목이
수학이었습니다
그리고 18살 때 과외를 시작했을 때
그 과목도 수학이었고
초등학교 5학년 때부터
스트레스를 받으면
수학 문제를 풀고 있는데요
다만 제가 고2 2학기 때부터
영어에 약간 美쳐서
지금은 수학 문제도
영어로 보고 있습니다
안 하는 건 아니에요
그래서 오늘은 딱 두 분제를 풀려고 하는데
한 문제는 초등 5학년 수학 기초에 맞는
평행사변형의 넓이 공식 문제이고
다른 하나는
삼각비 특수각을 알아야 풀 수 있는
중등 수학 중학 수학 중3 수학의
문제입니다
둘 다 잼나요!
그럼 풀어보도록 하겠습니다!
go go go ~

초등 5학년 수학 기초
평행사변형 넓이 공식
중등 수학 중학 수학
중3 수학 삼각비 특수각
1. 초등 5학년 수학 기초
평행사변형 넓이 공식
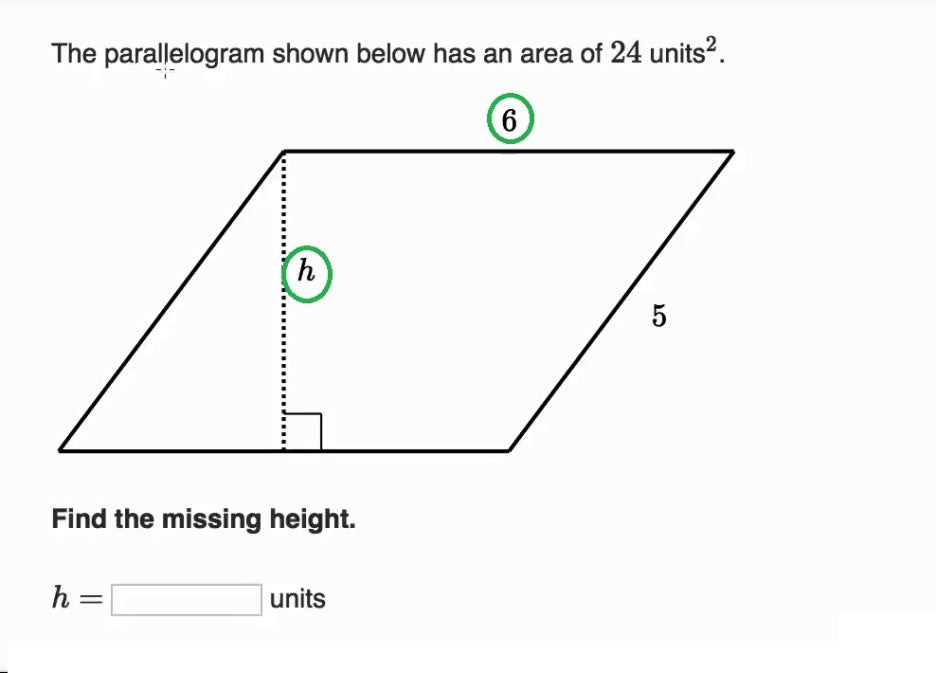
먼저 초등 5학년 수학 기초 수준의
문제를 살펴보면
밑변을 주어주고
높이를 구해라 라는 문제가 나옵니다!
이런 문제는
평행사변형 넓이 공식
하나만 알면 끝나죠?
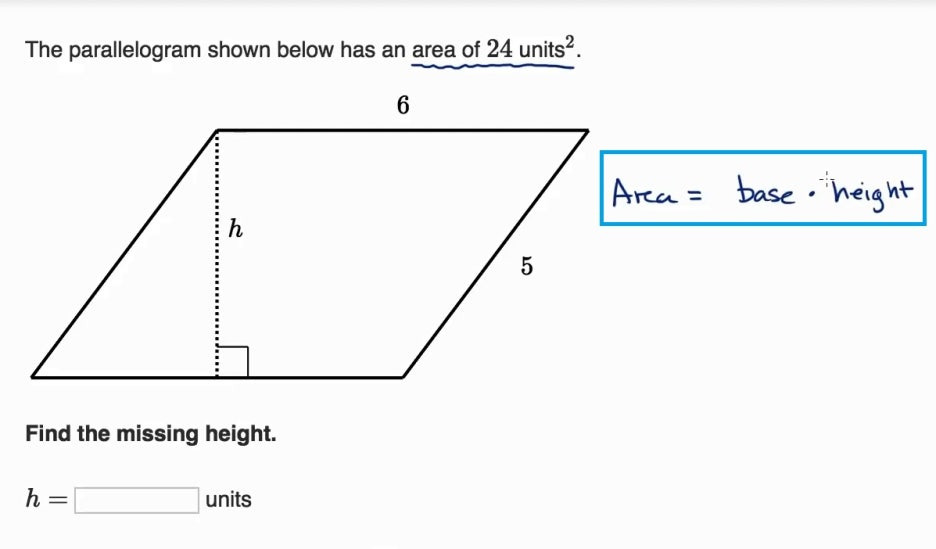
근데
평행사변형의 넓이 공식은
밑변 *높이입니다.
그리고 밑변이란
높이 밑에 있는 변이에요
그래서 이 문제는
1) 평행사변형의 넓이 공식 알고
2) 어떤 게 밑변이냐만 알면
술술 풀리는 거죠!
높이를 h 라고 했을 때
h 에 닿아 있는 밑변과 길이가 같은 게
위에 있는 6이죠?
이건 평행사변형의 성질을
이용하시면 되는 부분입니다.
평행사변형이란?
서로 마주 대하는 두 쌍의 변이
각각 평행인 사각형인데
* 평행사변형의 성질
평행사변형에서 두 대각선은
서로 다른 대각선을 이등분 한다.
두 쌍의 대변의 길이는 각각 같다
두 쌍의 대각의 크기가 각각 같다.
출처 입력
이러한 성질을 갖게 되고
우리에게 필요한 걸 길이이기 때문에
두 쌍의 대변의 길이는 각각 같다!
사실 이 부분은 '평행' 배울 때
이미 이해하고 넘어 왔어야 하는 부분입니다.
따라서 평행사변형의 성질에 의해서
밑변이 6이 되는 거고
평행사변형의 넓이 공식에 의해서
24 = 6h
그러므로 높이는 4가 됩니다.
엄청 쉽죠?
근데 전직 수학 과외교사로서 ㅋㅋ
어떤 게 정의이고 어떤 게 성질인지
이거 정확하게 보셔야 돼요!
특히 도형은 그렇습니다
평행사변형은 평행 까지만 조건이고
평행의 성질에 의해서 생긴
평행사변형의 성질 덕분에
밑변을 구할 수 있었습니다.
이런 거 빈칸 문제로 잘 나오잖아?
제가 잡아줬던 생각이 나요...
그럼 여기서
초등 5학년 수학 기초 평을 마치고
이제 중등 수학 중학 수학
중3 수학 삼각비 특수각이 필요한
평행사변형의 넓이 공식 문제
로 들어가 볼까요?
2. 중등 수학 중학 수학
중3 수학 삼각비 특수각
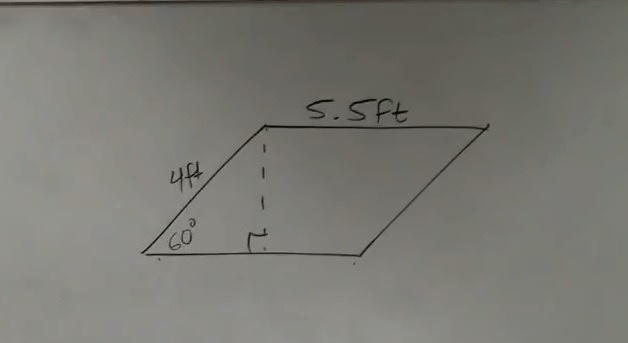
초등 5학년 수학 기초 문제와
확연히 다른 부분은?
각도가 나와 있다는 거죠?
그럼 각도를 가지고 풀라는 거고..
삼각비 특수각 문제라는 건데
다들 기억나시나요?
1 : 1 : √2 (45도)
2 : 1 : √3 (60도)
3: 4 : 5
5 : 12 : 13
8 : 15: 17
그리고 이건
피타고라스 의 수
그냥 같이 기억하면 편해요.
이거죠?
아직도 생각이 나긴 하네?
긑데 밑에 3개는
a² + b² = c²
이용하면 되는 건데
위의 2개는 각이 조건으로 붙죠
그리고 우리가 필요한 건 이겁니다!
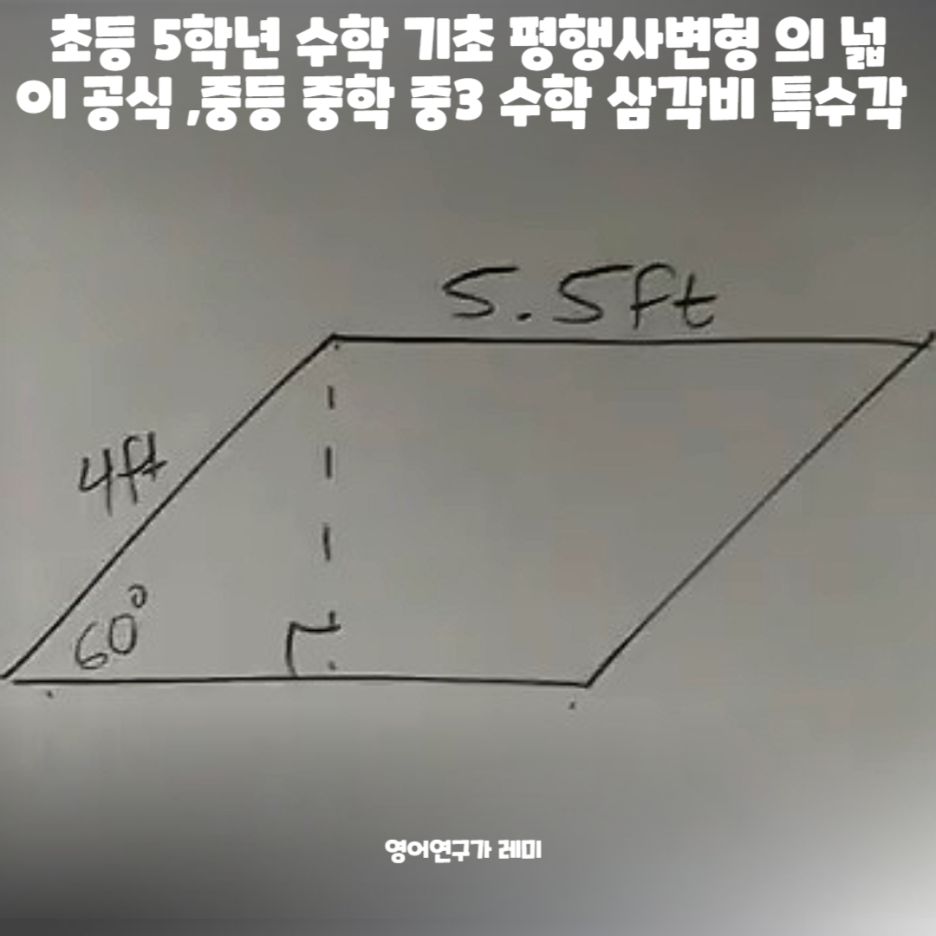
다시 그림을 좀 보면...
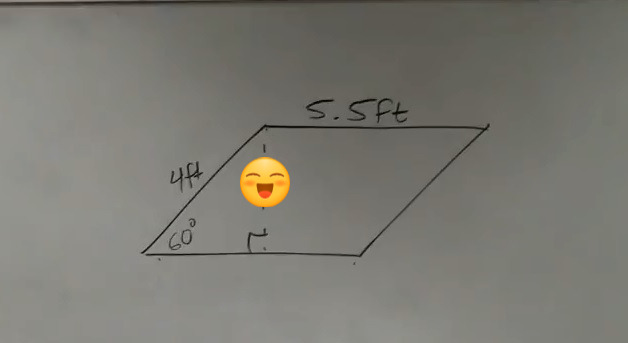
바로 저 웃는 부분이
높이잖아요?
이걸 구하라는 건데
각도 하나 주고 변 하나 줬으면....
5.5 는 나중에 넓이 계산할 때 필요한 거고
비율 비용하라는 겁니다!
60도가 나오면?
2 : 1 : √3 이죠!
90도 : 30도 : 60도
그럼 가+장 긴 변이 4피트이니까
이 친구가 2가 되는 거죠?
그리고 우리가 구할 부분은
60도에 대응하는 부분입니다
√3이죠!
2 : 1 : √3
4 : 2 : 2√3
그러니 저 높이는?
2√3이네요.
따라서 평행사변형의 넓이 공식에
대입을 하면
넓이 = 높이 *밑변
= 5.5 * 2√3 = 19.05 피트가
나오게 됩니다
√3 값에 1.731818182.....
을 입력한 값입니다
(그냥 1.732 곱하고 싶다!)
오늘은
초등 5학년 수학 기초
평행사변형 넓이 공식
중등 수학 중학 수학
중3 수학 삼각비 특수각
에 대해서 공부를 해봤는데요
증명까지 하려면 복잡하고
그냥 두 문제 가볍게 풀어봤습니다!
같은 평행사변형의 넓이 공식
문제라고 해도
역시 학년이 다르니까 느낌이 좀 다르죠?
참고로 저는
피타고라스를 좋아합니다
철학자로서도!
레미였습니다!
감사합니다!!!!
'교육일상' 카테고리의 다른 글
| 구글 렌즈 사용법! 사진 위치 찾기 간단하게 해보자! (0) | 2025.05.10 |
|---|---|
| 미우새 수학문제 : 예쁜 영어단어 팩토리얼 뜻! factorial 초등 2학년 수학 기초 고1 고등 수학 공부법 (0) | 2025.04.14 |
| 2025년 을사년 무슨 해? 띠 순서 십이간지 자축인묘진사오미신유술해 갑을병정무기경신임계 색 12간지 (0) | 2025.04.14 |
| 삼재띠 계산법 : 삼합, 방합 등을 알아야! (들삼재, 눌삼재, 날삼재) 2025년 ~ 2036년 삼재띠까지! (0) | 2025.04.14 |
| 2026 월드컵 개최국 : 북중미 미국 캐나다 멕시코 16개 도시 그리고 경기장!! (0) | 2025.04.14 |



